TEMA 7. INTRODUCCIÓN A LA BIOESTADÍSTICA

Durante el tema 7, comenzamos a ponernos en marcha con los problemas y para ello lo primero que debíamos saber el concepto de estadística. La estadística es el cuerpo de conocimientos para aprender de la experiencia, frecuentemente en de forma de números provenientes de medias que muestran variaciones entre los diferentes individuos. Parte del supuesto de que las características clínicas que se observan cambian de un paciente a otro: las variable. Éstas pueden ser de dos tipos según el punto de vista de la medición. 

En primer lugar se encuentran las variables cualitativas que se refieren a propiedades que no pueden ser medidas como el nivel de conocimientos o el estado civil y por otro lado variables cuantitativas que miden términos numéricos. Éstas últimas pueden ser discretas si solo pueden tomar un número finito de valores como el número de hijos, o continuas si pueden ser divididas de forma infinita como la talla, la tensión arterial etc.. 
Ambas categorías deben ser exhaustas y exclusivas.

Una vez que tenemos diferenciadas las variables, es hora de ponerlas ordenadas y de forma visiblemente clara representando los datos, y esto es elaborando una tabla de frecuencia. Para ello os pongo un ejemplo y os detallo cómo hay que hacerlo.

Por ejemplo, obtenemos los pesos en kg de niños atendidos en una consulta y queremos ordenarlos y clasificar en intervalos.

Pesos En Kg De Niños Atendidos En La Consulta De Niño Sano. N = 40

3,9            4,7          3,7        5,6       4,3        4,9    5,0       6,1        5,1     4,5

5,3            3,9          4.3        5.0       6.0        4.7    5.1       4.2        4.4     5.8

3.3            4.3          4.1        5.8       4.4        4.8    6.1       4.3        5.3     4.5

4.0            5.4          3.9        4.7       3.3        4.5    4.7       4.2        4.5     4.8

En primer lugar lo que haremos será buscar el peso mayor y el peso menor del grupo de datos para así averiguar el rango o recorrido de la muestra. En este caso:

El que más pesa tiene un peso de 6,1 Kg y el que menos pesa tiene un peso de 3,3 Kg, por lo que el recorrido es 6,1-3,3= 2,8

A continuación, para calcular el número de intervalos en los que los vamos a dividir le hacemos la raíz cuadrada al  número total de individuos de la muestra y vemos que la raíz de 40 es 6,32. Por tanto los clasificaremos en 6 intervalos.

Al ser el recorrido 2,8 lo dividiremos entre el número de intervalos para así saber la amplitud de dicho intervalo que en este caso será  2,8/6= 0,46

Tras estos pasos, podemos proceder a realizar la tabla de frecuencia.

Al ser variables continuas debemos poner paréntesis y corchetes en los extremos de cada intervalo para excluirlos del siguiente. 

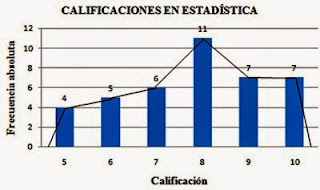
Como se observa, la fi o frecuencia absoluta es el número de niños de la muestra que se encuentran en ese intervalo de peso, y la Fi es la frecuencia absoluta acumulada que se averigua sumando los valores de fi. Ejemplo:  Fi 2=  3+8= 11, Fi 3= 11+14=25

La hi es la frecuencia relativa que se halla dividiendo la frecuencia absoluta entre el número total de la muestra (fi/N). La Hi es el porcentaje y para comprobarlo debemos sumarlos todos y que el resultado sea el 100%.

Otro punto importante del tema es la representación de gráficas, que son la imagen de las ideas o forma de representación numérica. Entre las más importantes destacan: el diagrama de barra, el pictograma (variante del diagrama de barra), el histograma, el gráfico de tronco y hojas, gráfico de sectores y finalmente el gráfico para datos bidimensionales y multidimensionales.

Para no extenderme mucho voy a hacer un pequeño resumen de lo más importante de cada uno.

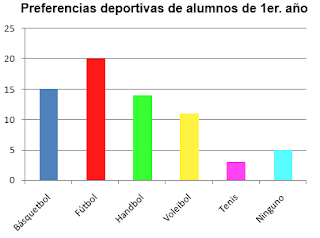
• Diagrama de barra                    Se utilizan para medir variables cualitativas, nominales y policotómicas. Una variante de      éste es el pictograma que se diferencia del diagrama en que se sustituyen las barras por iconos  referidas a lo que estamos estudiando pero no aportan información adicional.

• Histograma y polígonos        de frecuencia                           Solo se usa para variables continuas y en este caso los dos ejes no proporcionan información. Si la amplitud del intervalo es la misma, las columnas irán juntas, de lo contrario habrá que ajustar el área del rectángulo según una proporción.

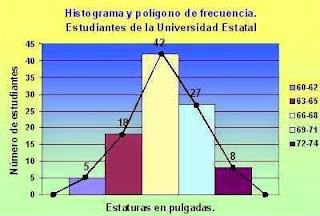
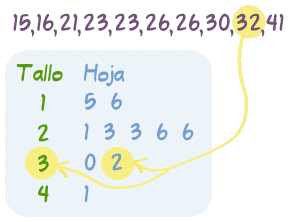
El polígono de frecuencia se realiza  haciendo las marcas de clase que es el resultado de la media entre la suma de los dos extremos de cada intervalo.

• Gráfico de tronco (o tallo) y hojas              Se utiliza para expresar variables cuantitativas continuas. Es un híbrido  entre la tabla y el  histograma: nos muestra la forma de la distribución y  los valores de la variable. Cada dato de la seria se divide en tres partes:  tronco(decenas), las ramas (centenas) y la hoja (unidades).

• 
  Gráfico de sectores                                                                           Se utilizan para variables cualitativas y con pocas categorías preferentemente dicotómicas.

• Gráfico de datos bidimensionales y multidimensionales                                                                                                                                   
  
  Son gráficos en los que se representan varias variables al mismo tiempo. Suelen mezclar variables cualitativas y continuas.

Diagrama de estrella (estadística avanzada)